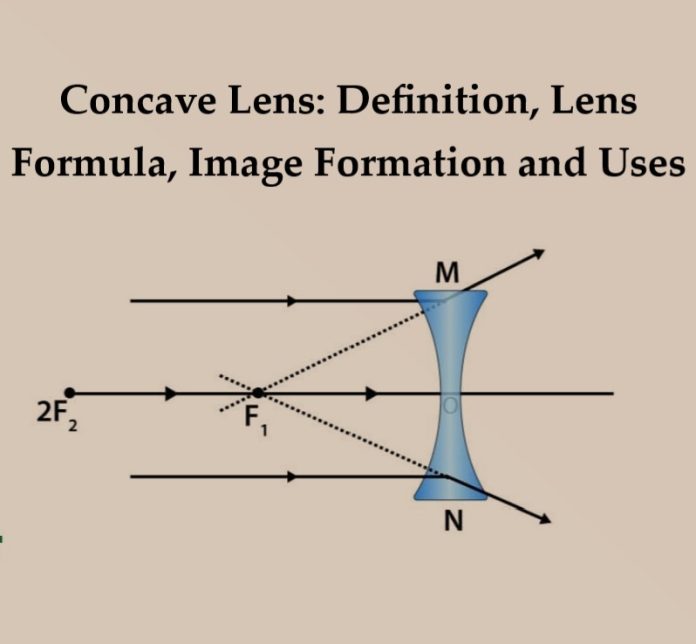
Concave Lens
We have been able to achieve some astounding pretty things with lenses over many centuries of living human beings. Although we don’t know when or when the first person discovered the concept of the lens, it is evident that at some point in history, the people of ancient times, most likely from the Near East, learned that they could easily alter the term light by using a shaped piece of glass.
As people discovered that they could accomplish different things by utilizing different lens shapes, how and for what lens purposes were utilized continued to increase day by day over the later ages or centuries.
For decades, humans have used lenses to do a variety of things. From making something appear larger to making something appear closer, lenses can be used for a variety of purposes. They’ve been doing this without knowing the many sorts of lenses or their characteristics, among other things. People used to think that lenses were just bits of glass that could alter light. Years later, the lenses were divided into two groups. They are as follows:-
- Convex Lens
- Concave lens
Here let’s look closely into the Concave lens and its characteristics, formula, image formation and uses in detail.
What is a Concave Lens?
A concave lens diverges a straight light beam from the source to produce a reduced, upright virtual image. It can generate both physical and virtual images. At least one inward curved surface is present on the concave lens. A diverging lens is a concave lens that is shaped round inwards in the centre and bulges outwards through the edges, causing light to diverge. They are used to treat myopia by making distant objects appear smaller than they are.
Concave Lens Formula
The concave lens formula is used to determine the nature and position of the image created by the lens. The following is the lens formula:
1/f= 1/v+1/u
where,
f = focal length
v = Image’s distance from the centre
u = Object’s distance from the centre.
Similarly, the image magnification is provided by the equation,
M= hi/ho=v/u
where,
M = magnification
hi = height of the image
ho = height of the object.
Also Read: वोटर आईडी को आधार कार्ड से लिंक करें/जोड़ें: 2 minutes में घर बैठे
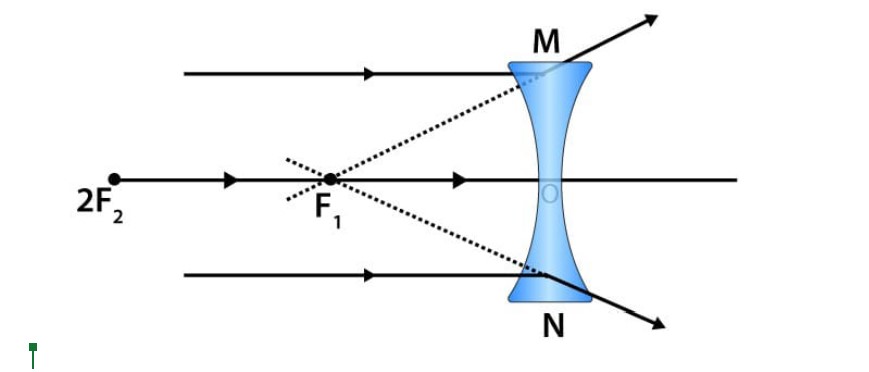
Image Formation in Concave Lens
An object positioned at infinity creates a virtual image at the focus. The image is substantially smaller in size than the object.
Image formation1:
https://docs.google.com/document/d/1bTJhGirmZDP5sIYf34NqPjpBncQ5nUi20epEH8iGO60/edit?usp=sharing
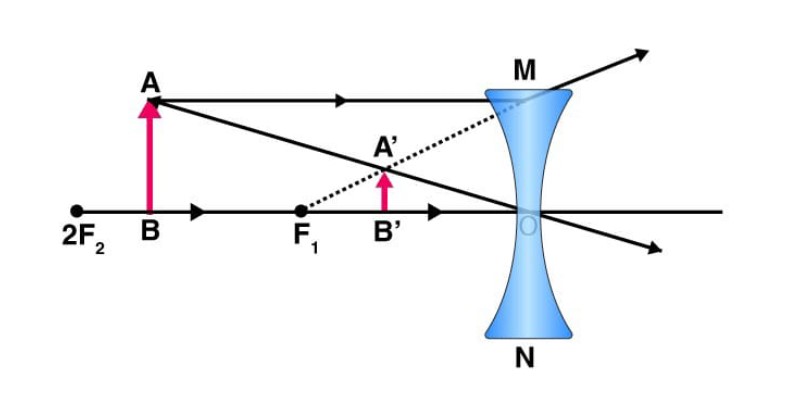
Source: byjus.com
An object at a finite distance from the lens produces a virtual image between the pole and the focus of the convex lens. As a result, the image is less in size than the thing.
Image formation2:
https://docs.google.com/document/d/1SXAVAUyTk31-HoiTP11FsqebJodEjcaAbB1Md0PzCwE/edit?usp=sharing
Source: byjus.com
Uses of Concave Lens
The following are some examples of applications:
Used in Telescope
In telescopes and binoculars, these are used to magnify objects. Because a convex lens causes blurring and distortion, telescope and binocular manufacturers put concave lenses before or in the eyepiece to improve focus.
Used in Eye Glasses
These are often used to cure myopia, also known as nearsightedness. Myopia causes the eyeball to be overly long, and images of distant objects fall short of the retina. As a result, concave lenses are utilized in spectacles to compensate for the shortage by spreading out the light rays before they reach the eyeball. This improves the person’s ability to see distant objects clearly.
Used in Peepholes
Peepholes, sometimes known as door viewers, are security devices that provide a 360-degree view of items beyond walls or doors. It is used to reduce the proportions of objects while providing a wider view of the object or area.
Disclaimer: This post is for educational purpose.